Notre série d’articles consacrée à l’exploration autonome au service des robots mobiles fait sa rentrée ! Pour ce troisième épisode, l’équipe Awabot Intelligence décortique l’exploration basée sur les frontières, qui s’est imposée en tant que méthode de référence suite au comparatif publié dans l’article précédent.
Principe de l’exploration autonome basée sur les frontières
Pour rappel, cette méthode implique que la solution robotique mobile explore l’environnement en se déplaçant continuellement vers de nouvelles frontières.
Comprendre les concepts de grille d’occupation et de frontière
Pour comprendre l’algorithme basé sur les frontières, il faut d’abord définir deux concepts : la grille d’occupation et la frontière.
Une grille d’occupation est une façon de représenter l’environnement. Elle décompose l’espace en un ensemble de cellules de même taille. Ces cellules stockent une probabilité d’occupation qui peut être utilisée pour déterminer si l’espace correspondant à chaque cellule est libre, occupé ou inconnu.
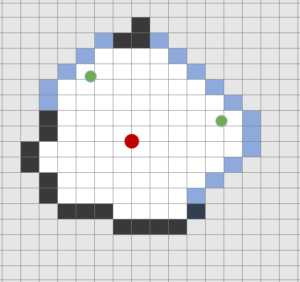

La zone qui délimite l’espace libre de l’espace inconnu est appelée frontière. Chaque frontière est représentée par :
- une liste de cellules libres adjacentes ;
- une taille : le nombre de cellules contenues dans une frontière ;
- une distance : la distance euclidienne, qui correspond à la distance la plus courte, entre le robot et la frontière (en mètres) ;
- une orientation : l’angle entre la direction du robot et la frontière candidate (en degrés) ;
- un centroïde : le point au centre des masses de la frontière ;
- un coût : le coût calcule l’intérêt d’une frontière à être visitée.
Comment le robot choisit-il la prochaine frontière ?
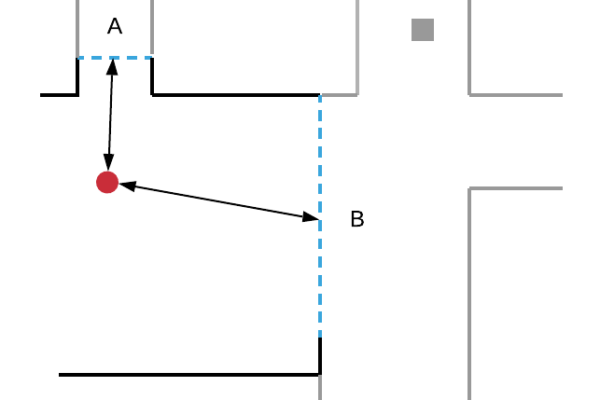
Supposons un robot mobile dans un environnement inconnu détectant deux frontières A et B. Comment le robot choisit-il la prochaine frontière à visiter ?
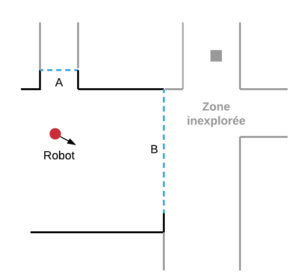
Exemple de frontières détectées par un robot
Le principe est simple : le robot va tout simplement choisir la frontière qui a le plus faible coût parmi les frontières candidates.
Dans notre étude, la notion de de coût est établie selon la fonction suivante :
C(ƒ) = λ1distance(ƒ) – λ2taille(ƒ) + λ3orientation(ƒ) (1)
[Gao et al., 2004]
Avec :
- ƒ : une frontière de F
- λ1, λ2 et λ3 : les coefficients (paramètres de poids normalisés) entre 0 et 1
Selon l’équation (1), une frontière intéressante à visiter, c’est-à-dire avec un coût relativement faible, est une frontière proche du robot, de grande taille et qui se situe face à lui.
L’objectif est que le robot explore un environnement en entier en un minimum de temps et en utilisant le moins de ressources possible :
- si une frontière est proche, le robot va y accéder en moins de temps et en utilisant moins de ressources énergétiques ;
- si une frontière est grande, alors il y a de fortes chances pour qu’une grande zone inexplorée de taille conséquente se trouve au-delà de celle-ci. On va donc acquérir plus d’informations sur l’environnement ;
- si une frontière se trouve face au robot, cela lui évite de perdre du temps dans la rotation.
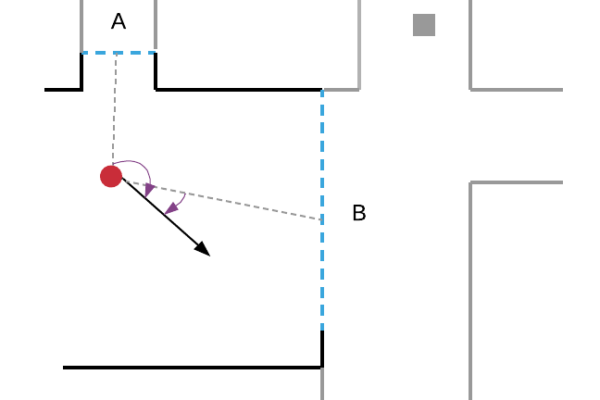
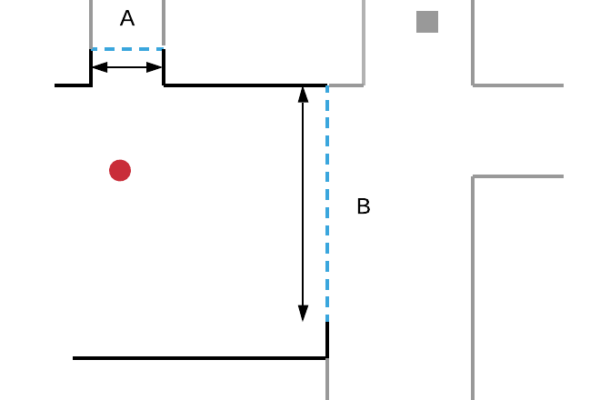
Afin d’illustrer ces notions, les schémas (a), (b) et (c) ci-dessous décomposent les frontières selon les trois critères de distance, de taille et d’orientation. En particulier, on observe que la frontière A est plus proche du robot que la frontière B, mais plus petite et avec un angle par rapport au robot plus élevé.
Pour trouver un compromis entre la distance, la taille et l’orientation, on utilise les paramètres de poids λ1, λ2 et λ3 : mettre davantage de poids sur un des facteurs permet de prioriser celui-ci. Dans notre étude, ces valeurs ont été fixées grâce à des tests réalisés sur grille de paramètres (i.e., gridsearch).
Exploration autonome basée sur les frontières : présentation de l’algorithme
La première étape consiste à détecter des frontières à l’aide des capteurs du robot (capteur LiDAR dans notre cas). L’algorithme parcourt la grille d’occupation et identifie toutes les cellules libres adjacentes à des cellules inconnues, ce qui donne des frontières candidates. Parmi ces frontières candidates, il sélectionne celle qui a le coût le plus faible selon l’équation (1) et récupère son point centroïde qui devient la nouvelle destination du robot (algorithme 1).
Algorithme 1 : Exploration des frontières
1: G ← Grille d’occupation
2: Faire
3: F = DétecterFrontières(G)
4: D = SélectionnerFrontière(F)
5: Tant que F n’est pas vide
6: Fin Tant que
L’algorithme d’exploration des frontières est répété toutes les secondes. Régulièrement, le robot détecte de nouvelles frontières à partir de la grille d’occupation construite et sélectionne une nouvelle destination à atteindre pour obtenir de nouvelles informations sur son environnement. L’algorithme se termine lorsque le robot ne détecte plus de nouvelle frontière, c’est-à-dire lorsque tout l’espace est supposé connu.
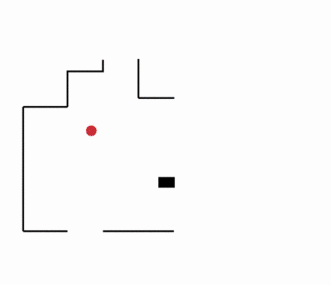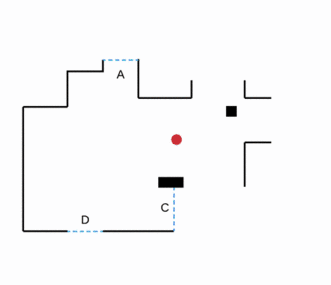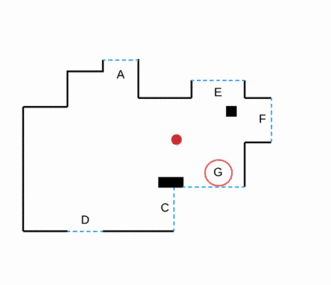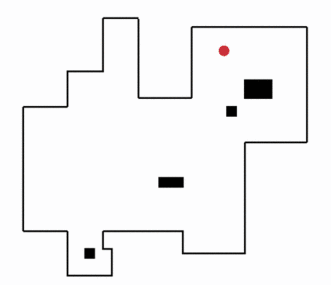
Exploration autonome basée sur les frontières
Mise en oeuvre
Cette solution a été mise en œuvre sur le robot Turtlebot3 Burger grâce au middleware Robot Operating System (ROS) et au logiciel Gazebo qui permet de simuler le robot et les environnements.
Vous souhaitez en savoir plus sur les tests et résultats obtenus par cette solution d’exploration autonome au service des AMR ? Rendez-vous le mois prochain !